P2 de Álgebra Linear I - 2001.1

Data: 16 de maio de 2001.

1) Considere os vetores

$$u_1=(1,1,1), \quad u_2=(1,1,0), \quad u_3=(3,3,2), \quad u_4=(2,2,2)$$

e o subespaço vetorial V gerado por u₁, u₂, u₃e u₄.

a) Determine uma base 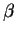$\beta$ de V.

b) Determine uma base ortogonal 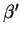$\beta^\prime$ de V.

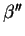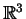c) Determine uma base ortogonal $\beta^{\prime \prime}$ de $\mathbb{R} ^3$que contenha $\beta^\prime$.

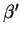d) Veja se (2,2,4) pertence a V.

e) Escreva o vetor (5,5,3) como combinação linear dos vetores da base $\beta$.

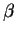2) Considere as transformações lineares

$$T(x,y)=(x+3y, 2x +4y), \quad S(x,y)=(5x+7y, 6x +8y).$$

Determine explicitamente as matrizes das transformações lineares T, S, 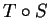$T\circ S$ e $S\circ T$.

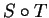3) Considere a transformação linear 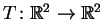$T\colon \mathbb{R} ^2 \to \mathbb{R} ^2$definida como a projeção ortogonal na reta $r\colon \{(t,3t), \, t\in \mathbb{R}\}$.

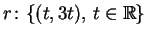a) Determine a matriz de T.

b) Calcule T(1,3) e T(-3,1).

4) Considere o vetor 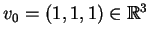$v_0=(1,1,1)\in \mathbb{R} ^3$ e defina a transformação linear

$$T\colon \mathbb{R} ^3 \to \mathbb{R} ^3, \quad T(v)=v\times v_0.$$

a) Determine o conjunto dos vetores v tais que T(v)=0.

b) Estude se existe algum vetor v tal que T(v)=v₀.

c) Estude se existe algum vetor v tal que T(v)=v.

d) Determine a forma geral de T e sua matriz [T].

e) É T inversível?