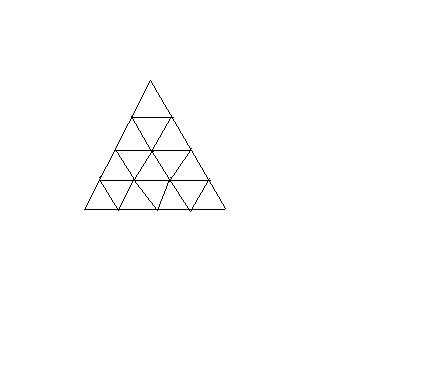
Pessoal, ontem mandei uma dúvida sobre contar o total
de triângulos de todos os tamanhos de uma figura como
a que enviei abaixo novamente. Pensei muito sobre esse
problema e cheguei a uma fórmula não muito amigável,
mas até que não é ruim. Já dá até pra escrever um
algoritmo pra rodar no computador se quiser.
Primeiro, eu chamei de x o número de lados de
triângulos que temos na base. Por exemplo, se tivermos
um triângulo só x = 1.
/_\
Se tivermos uma figura com quatro triângulos de menor
tamanho, temos:
/_\
/_\ /_\
x = 2
Na figura que mandei, temos x = 4.
Com isso, já que você tem triângulos de diferentes
tamanhos, você deve contar separadamente os triângulos
que têm como lado 1 traço, 2 traços, 3 traços...E
depois tem que contar os triângulos que estão de
cabeça pra baixo com esses mesmos tamanhos.
Se você fizer isso em função dos traços da base não
fica muito ruim. Todas as linhas vou escrever a soma
de várias parcelas de x menos alguma coisa. Quando
você for calcular para algum x, você vai fazer as
subtrações até encontrar o valor zero, aí você para.
Por exemplo, na primeira linha temos:
x + (x - 1) + (x - 2) + (x - 3) + ...
Se você tiver x = 2, você irá somar até x + (x - 1),
porque o próximo dará zero e aí você deve parar.
Bom, no final você encontra isso:
triângulos de lado 1:
cabeça pra cima = x + (x - 1) + (x - 2) + (x - 3) +
...
cabeça pra baixo = (x - 1) + (x - 2) + (x - 3) + ...
total = x + 2.[(x - 1) + (x - 2) + (x - 3) + ...]
É como se o triângulo maior de todos fosse dividido em
várias linhas, aí você vai contando de cada linha.
triângulos de lado 2:
cabeça pra cima = (x - 1) + (x - 2) + (x - 3) + (x -
4) + ...
cabeça pra baixo = (x - 3) + (x - 4) + (x - 5) + ...
total = (x - 1) + (x - 2) + 2.[(x - 3) + (x - 4) +
...]
Por que aqui começamos a ter de cabeça pra baixo só
com (x - 3)? Porque para termos um triângulo de cabeça
pra baixo, o triângulo maior tem que ter o dobro de
traços na base do que o tamanho do triângulo. Como
esse tem lado 2, precisamos ter x = 4, que se fizermos
(x - 3) dará 1. Enquanto x for menor que 4 esse número
será negativo ou zero e aí não vamos contar.
triângulos de lado 3:
cabeça pra cima = (x - 2) + (x - 3) + (x - 4) + (x -
5) + ...
cabeça pra baixo = (x - 5) + (x - 6) + (x - 7) + ...
total = (x - 2) + (x - 3) + (x - 4) + 2.[(x - 5) +
...]
E assim teremos sempre esse padrão. Os triângulos de
cabeça pra cima começam sempre com (x - a), onde "a" é
o número anterior ao tamanho do triângulo. E os
triângulos de cabeça pra baixo começam sempre com x -
(2a - 1). Depois os outros termos você vai tirando
sempre 1.
No final das contas você pode somar tudo isso. Soma os
triângulo de cabeça pra cima com os de cabeça pra
baixo de todos os tamanhos. O problema é que não pode
desenvolver muita coisa, porque não pode misturar x -
3 com x - 4, porque se você tiver x = 4, você não terá
o termo x - 4. Mas somando apenas x - 1 com x - 1 e x
- 2 com x -2, você terá:
total = x + 3.(x - 1) + 4.(x - 2) + 6.(x - 3) + 7.(x -
4) + 9.(x - 5) + 10.(x - 6) + 12.(x - 7) + 13.(x - 8)
+ ...
No final você tem então todos os fatores x, x - 1, x -
2, x - 3, ... e os coeficientes de cada um têm uma
ordem até boazinha:
1, (pula o 2), 3, 4, (pula o 5), 6, 7, (pula o 8), 9,
10, (pula o 11), 12, 13, (pula o 14), ...
E você vai usar a fórmula até o termo em que quando
fizer a diferença de x com alguma coisa dê zero. Ou
você pode até fazer a seguinte regra: considere que
desse valor total você vai pegar apenas os x primeiros
termos.
Por exemplo, vamos pegar o triângulo da figura que tem
4 traços na base, ou seja x = 4. Então vamos pegar até
o quarto termo dessa fórmula e fazer x = 4:
total = x + 3.(x - 1) + 4.(x - 2) + 6.(x - 3)
total = 4 + 3.(4 - 1) + 4.(4 - 2) + 6.(4 - 3)
total = 4 + 3.3 + 4.2 + 6.1
total = 4 + 9 + 8 + 6
total = 27
E aí você pode fazer pra qualquer x. Aquele menor que
tinha x = 2, só pegamos os 2 primeiros termos:
total = x + 3.(x - 1)
total = 2 + 3.(2 - 1)
total = 2 + 3.1
total = 2 + 3
total = 5
De qualquer jeito você não precisa ficar contando um
por um e correr o risco de se perder mais facilmente.
Mas o meu problema agora é o seguinte. Suspeito que
ainda dê para simplificar a fórmula, considerando duas
fórmulas, uma para quando x é par e outra para quando
x é ímpar. Talvez simplifique, mas aí você tem duas
fórmulas, não sei. Ainda não consegui.
Será que alguém consegue melhorar daqui pra frente. O
pior acho que já passou.
Um abraço,
Rafael.
=====
Rafael Werneck Cinoto
ICQ# 107011599
rwcinoto@yahoo.com
rafael.caixa@gov.com.br
matduvidas@yahoo.com.br
http://www.rwcinoto.hpg.com.br/
__________________________________________________
Do You Yahoo!?
LAUNCH - Your Yahoo! Music Experience
http://launch.yahoo.com
contatriang.gif